22. Parametric Surfaces and Surface Integrals
d. Applications of Scalar Surface Integrals
1. Surface Area
Finding surface area of any given surface, \(S\), is straightforward now that we have found \(dS\). We integrate \(dS\) over the entire surface to find the total area. \[ A=\iint_S \,dS =\iint_S |\vec{N}|\,du\,dv \]
Find the area of the polar ice cap, \(P\), on a planet of radius \(2\). Assume the arctic circle is at \(30\) degrees. The plot shows the ice cap in white.
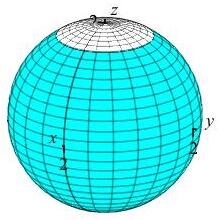
We need to know \(dS\) for spherical coordinates for a sphere of radius 2. Then we need the surface area of the piece of the sphere from \(\phi=0\) to \(\phi=30^\circ\).
The parametric equation for a sphere of radius \(2\) is \[ \vec R(\phi,\theta) =\left\langle 2\sin\phi\cos\theta,2\sin\phi\sin\theta,2\cos\phi\right\rangle \] From this equation we can find \(\vec{e}_\phi\) and \(\vec{e}_\theta\) (the radius \(\rho\) is not changing) \[ \begin{matrix} \quad \\ \vec{e}_\phi= \\ \vec{e}_\theta= \end{matrix} \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \left\langle 2\cos\phi\cos\theta\right. & 2\cos\phi\sin\theta & \left. -2\sin\phi\right\rangle \\ \left\langle -2\sin\phi\sin\theta\right. & 2\sin\phi\cos\theta & \left. \quad0\quad\right\rangle \end{vmatrix} =\vec{N} \] Notice how we added the \(\hat{\imath}\), \(\hat{\jmath}\), \(\hat{k}\) and the vertical bars to compute \(\vec N\): \[\begin{aligned} \vec{N} &=\vec{e}_\theta\times\vec{e}_\phi \\ &=\hat{\imath}(0--4\sin^2\phi\cos\theta) -\hat{\jmath}(0-4\sin^2\phi\sin\theta) \\ &\quad+\hat{k}(4\sin\phi\cos\phi\cos^2\theta--4\sin\phi\cos\phi\sin^2\theta) \\ &=\left\langle 4\sin^2\phi\cos\theta,4\sin^2\phi\sin\theta,4\sin\phi\cos\phi\right\rangle \end{aligned}\]
The normal vector for a sphere must be radially inward or outward. In other words, it is a multiple of the position vector. In particular, the vector, \(\vec{N}\), in our example can be rewritten as: \[ \vec{N}=2\sin\phi\left\langle 2\sin\phi\cos\theta,2\sin\phi\sin\theta,2\cos\phi\right\rangle \] which is a multiple of the position vector. This is a useful mental check when integrating over the surface of a sphere.
To find \(dS\), we need the length of the normal: \[\begin{aligned} |\vec{N}| &=\sqrt{16\sin^4\phi\cos^2\theta+16\sin^4\phi\sin^2\theta+16\sin^2\phi\cos^2\phi} \\ &=\sqrt{16\sin^4\phi+16\sin^2\phi\cos^2\phi} =\sqrt{16\sin^2\phi} =4\sin\phi \end{aligned}\] Not coincidentally, this is the same thing you would get if you calculated the spherical Jacobian for volume, \(\rho^2\sin\phi\). Using the length of the normal, we have the scalar differential of surface area is: \[ dS=|\vec{N}|\,d\phi\,d\theta=4\sin\phi\,d\phi\,d\theta \] So we can now compute the integral for the area: \[\begin{aligned} A&=\iint_P \,dS =\iint_P |\vec{N}|\,d\phi\,d\theta =\int_0^{2\pi}\int_0^{\pi/6} 4\sin\phi\,d\phi\,d\theta \\ &=2\pi\left[-4\cos\phi\dfrac{}{}\right]_0^{\pi/6} =8\pi\left(-\cos\dfrac{\pi}{6}+\cos0\right) =8\pi\left(1-\,\dfrac{\sqrt{3}}{2}\right) \end{aligned}\]
Find the area of the piece of the paraboloid \(z=\dfrac{x^2+y^2}{5}\) below \(z=5\). The length of the normal vector was found in a previous exercise.
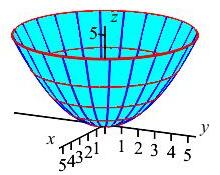
\(\displaystyle A=\iint_S 1\,dS=\dfrac{25\pi}{6}\left(5^{3/2}-1\right) \approx133.26\)
The paraboloid is parametrized by: \[ \vec R(r,\theta)=\left\langle r\cos\theta,r\sin\theta,\dfrac{r^2}{5}\right\rangle \] From the previous exercise, the length of the normal is: \[ |\vec N|=r\sqrt{\dfrac{4r^2}{25}+1} \] To find the limits on \(r\), we solve \(\dfrac{x^2+y^2}{5}=5\). So \(r=5\). So the area is: \[ A=\iint_S 1\,dS =\int_0^{2\pi}\int_0^5 r\sqrt{\dfrac{4r^2}{25}+1}\,dr\,d\theta \]
Notice that there is NO extra \(r\) in the integrand before the \(dr\,d\theta\)! This is because \(r\) and \(\theta\) are not actually polar or cylindrical coordinates. They are the parameters for a surface which just happen to have the same names. The \(|\vec N|\) plays the roll of the Jacobian and already contains an \(r\).
We continue the computation of the integral by making the substitution \(u=\dfrac{4r^2}{25}+1\) and \(du=\dfrac{8r}{25}\,dr\). To change the limits, we note, if \(r=0\) then \(u=1\) and if \(r=5\) then \(u=5\). So: \[\begin{aligned} A&=2\pi\dfrac{25}{8}\int_1^5 \sqrt{u}\,du =\dfrac{25\pi}{4}\left[\dfrac{2u^{3/2}}{3}\right]_1^5 \\ &=\dfrac{25\pi}{6}\left(5^{3/2}-1\right) \approx133.26 \end{aligned}\]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum